
Wir müssen unterscheiden
zwischen Theorie & Paxis!
Wir müssen unterscheiden
zwischen
Theorie & Paxis!
Reine Stimmung
Die Gleichstufige Stimmung basiert also auf einer logarithmischen Verteilung von Frequenzen und folgt damit nicht präzise den festen Saitenverhältnissen aus der Harmonielehre.
Um zu verstehen, weshalb die Gleichstufige Stimmung nun aber dennoch so gut in der Praxis funktioniert, kann man sie mit den „Reinen Stimmungen“ der Intervalle in der diatonischen Tonleiter vergleichen. Als „Reine Stimmung“ bezeichnet man ein zentrales musikalisches Tonsystem, welches auf Dur- und Moll-Dreiklängen basiert, die nur aus reinen Quinten und Terzen bestehen.
Die folgende Tabelle zeigt, dass die Abweichungen der Reinen Stimmungen zur Gleichstufigen Stimmung durchgehend in einem niedrigen Cents-Bereich liegen.
| Bezeichnung | Unter- kategorie | Stimmungsverhältnis | Gleichst. Stimmung | Tonleiter | ||||
| Dur-I/II | Moll-I/II | |||||||
| Prime | 1:1 | 0 ct | 0 ct | I | I | i | i | |
| Übermäßige Prime | Kleiner Chrom. Halbton | 25:24 | 71 ct | 100 ct | – | – | – | – |
| Großer Chrom. Halbton | 135:128 | 92 ct | – | – | – | – | ||
| Kleine Sekunde | Pythagoras | 256:243 | 90 ct | – | – | – | – | |
| Rein | 16:15 | 112 ct | – | – | – | – | ||
| Große Sekunde | Pythagoras | 10:9 | 182 ct | 200 ct | – | – | – | – |
| Rein | 9:8 | 204 ct | ii | ii | iio | iio | ||
| Kleine Terz | Pythagoras | 32:27 | 294 ct | 300 ct | – | – | – | – |
| Rein | 6:5 | 316 ct | – | – | III | III | ||
| Große Terz | Rein | 5:4 | 386 ct | 400 ct | iii | iii | – | – |
| Pythagoras | 81:64 | 408 ct | – | – | – | – | ||
| Quarte | 4:3 | 498 ct | 500 ct | IV | IV | iv | iv | |
| Übermäßige Quarte | Huygen | 7:5 | 582 ct | 600 ct | – | – | – | – |
| Rein | 45:32 | 590 ct | – | – | – | – | ||
| Pythagoras | 729:512 | 612 ct | – | – | – | – | ||
| Verminderte Quinte | Pythagoras | 1024:729 | 588 ct | – | – | – | – | |
| Rein | 64:45 | 610 ct | – | – | – | – | ||
| Euler | 10:7 | 617 ct | – | – | – | – | ||
| Quinte | 3:2 | 702 ct | 700 ct | V | v | v | V | |
| Kleine Sexte | 8:5 | 814 ct | 800 ct | – | – | VI | VI | |
| Große Sexte | Rein | 5:3 | 884 ct | 900 ct | vi | vi | – | – |
| Pythagoras | 27:16 | 906 ct | – | – | – | – | ||
| Kleine Septime | Natur | 7:4 | 969 ct | 1000 ct | – | – | – | – |
| Kleinere Reine/ Pythagoras | 16:9 | 996 ct | – | – | – | – | ||
| Größere Reine | 9:5 | 1017 ct | – | VII | VII | – | ||
| Große Septime | 15:8 | 1088 ct | 1100 ct | viio | – | – | viio | |
| Oktave | 2:1 | 1200 ct | 1200 ct | – | – | – | – | |
| Bez. | Stimmungs- verhältnis | Gleichst. Stimm. | |
| Prime | 1:1 | 0 ct | 0 ct |
| Kleine Sekunde | 16:15 | 112 ct | 100 ct |
| Große Sekunde | 9:8 | 204 ct | 200 ct |
| Kleine Terz | 6:5 | 316 ct | 300 ct |
| Große Terz | 5:4 | 386 ct | 400 ct |
| Quarte | 4:3 | 498 ct | 500 ct |
| Über- mäßige Quarte | 45:32 | 590 ct | 600 ct |
| Ver- minderte Quinte | 64:45 | 610 ct | |
| Quinte | 3:2 | 702 ct | 700 ct |
| Kleine Sexte | 8:5 | 814 ct | 800 ct |
| Große Sexte | 5:3 | 884 ct | 900 ct |
| Kleine Septime | 9:5 | 1017 ct | 1000 ct |
| Große Septime | 15:8 | 1088 ct | 1100 ct |
| Oktave | 2:1 | 1200 ct | 1200 ct |
Hinweis: In der Desktop-Ansicht dieser Tabelle finden sich ausführlichere Details zu verbreiteten Stimmungsverhältnissen und eine zusätzliche Verknüpfung mit den Dur- und Moll-Tonleitern.
„Reine“ Stimmung
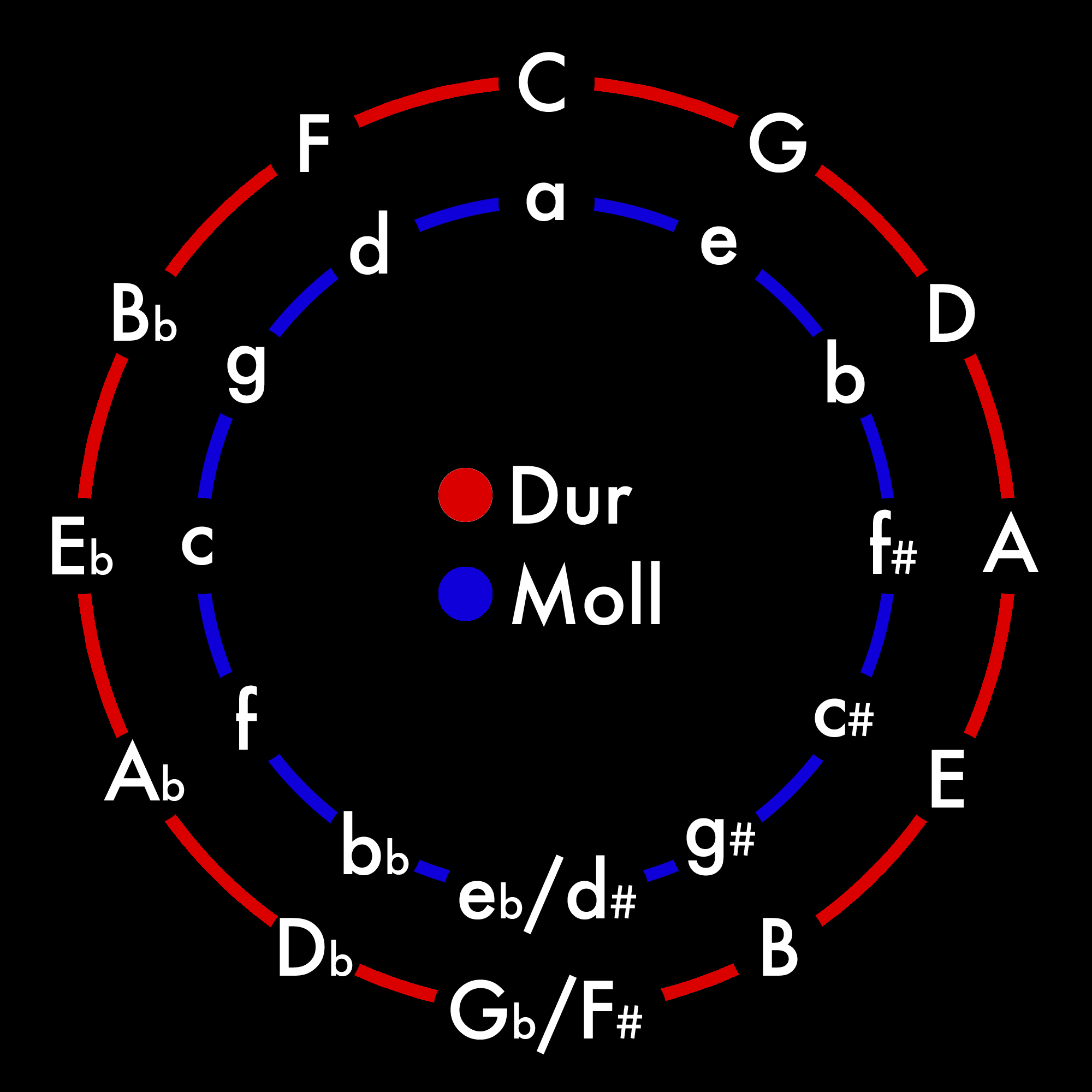
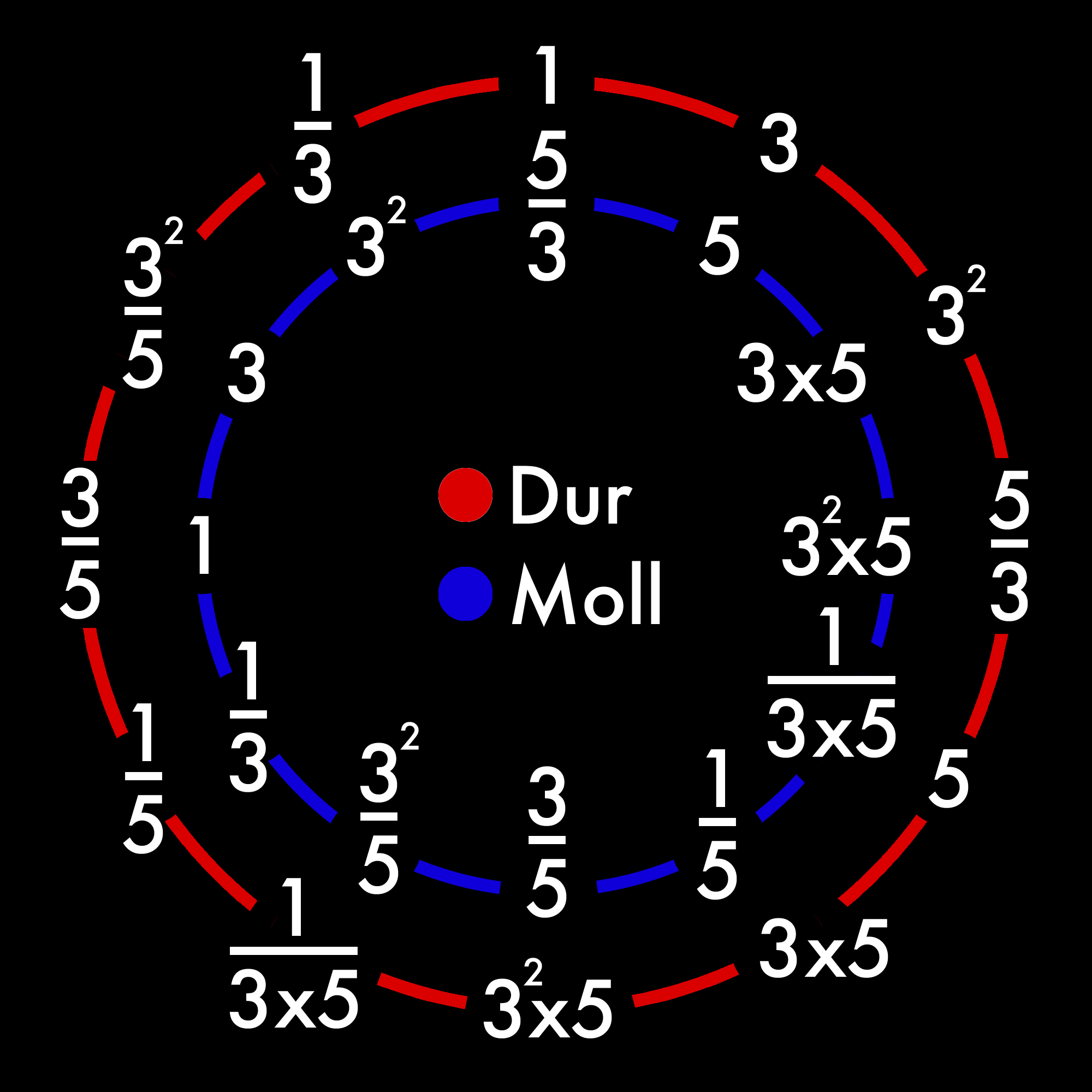
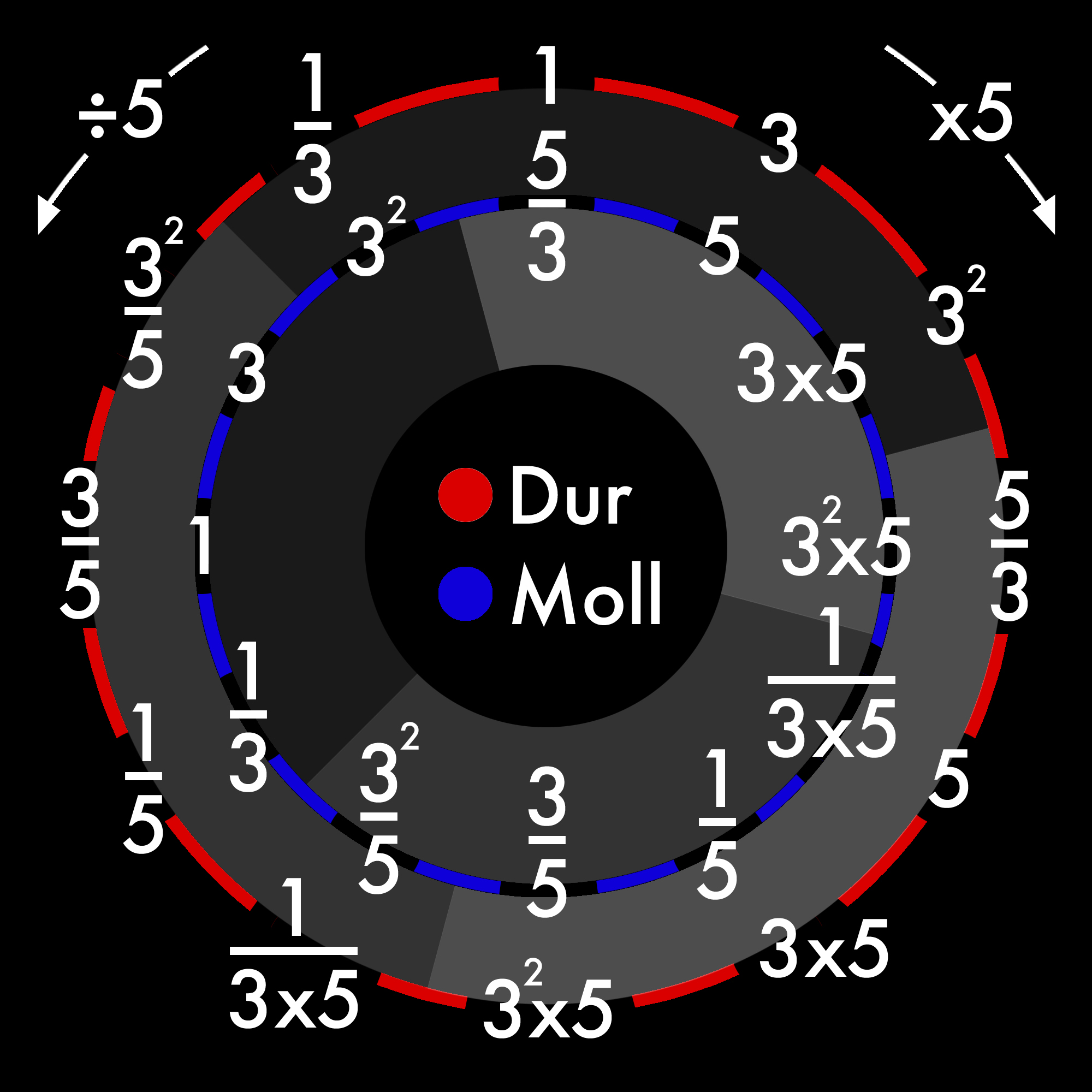
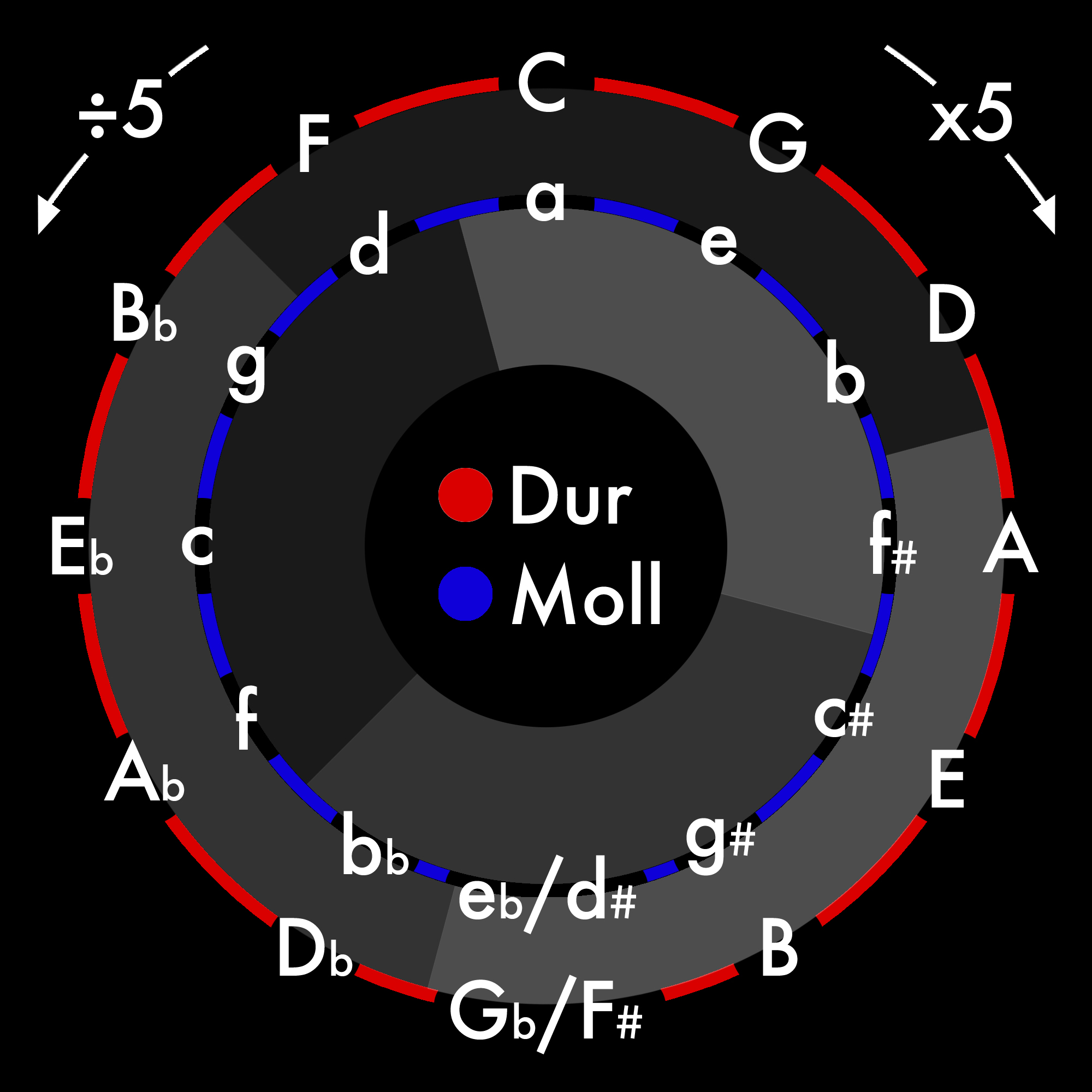
Stellt man die Saitenverhältnisse der Reinen Stimmung (zur Vereinfachung ohne Normierung der Oktave durch Vielfache von Zwei) im Quintenzirkel (am Beispiel ausgehend von der Tonart „C“) dar, ergibt sich ein klares Muster.
Folgende Darstellung zeigt, dass die Reine Stimmung aus jeweils drei Bereichen aufgebaut ist, die sich von einem Zentrum aus um den Faktor 5 unterscheiden (Verschiebung um eine Terz).
Außerdem sieht man, dass jeder Bereich aus vier Tönen besteht, die sich fortschreitend um den Faktor 3 unterscheiden (Verschiebung um eine Quinte).




„Reine“ Akkorde
Der Aufbau der Reinen Stimmung aus Quinten und Terzen steht im Zusammenhang mit den folgenden Saitenverhältnissen, aus welchen sich die „reinen“ Dur- und Moll-Akkorde zusammensetzen.
| Bezeichnung | Abkürzung | Akkord | Stimmungsverhältnis |
| Großer Septakkord | Dur(-I) | I – iii – V – viio | 8:10:12:15 |
| Dominantseptakkord | Dur-II | i – III – v – VII | 20:25:30:36 |
| Mollseptakkord | Moll(-I) | i – III – v – VII | 10:12:15:18 |
| Mollseptakkord mit großer Septime | Moll-II | i – III – V – viio | 40:48:60:75 |
| Bez. | Akkord | Stimm.- verhältnis |
| Dur(-I) | I – iii – V – viio | 8:10:12:15 |
| Dur-II | I – iii – v – VII | 20:25:30:36 |
| Moll(-I) | i – III – v – VII | 10:12:15:18 |
| Moll-II | i – III – V – viio | 40:48:60:75 |
Der Große Septakkord (engl. „Major (Major) Seventh Chord“) („Dur“ oder „Dur-I“) und der Mollseptakkord (engl. „Minor (Minor) Seventh Chord“) („Moll“ oder „Moll-I“) entsprechen den Standard-Akkorden, welche bereits in vorangegangenen Kapiteln beschrieben wurden und in den populären „Four Chords“-Akkordfolgen verwendet werden.
Währenddessen bauen die Varianten des Dominantseptakkords (engl. „Major Minor Seventh Chord“) („Dur-II“) und des Mollseptakkords mit großer Septime (engl. „Minor Major Seventh Chord“) („Moll-II“) auf einem verringerten bzw. erhöhten Leitton und einer entsprechend angepassten Tonleiter auf.
„Reine“ Spielbare Akkorde
Stellt man diese Akkorde mit ihren Stimmungsverhältnissen (zur Vereinfachung ohne Normierung der Oktave durch Vielfache von Zwei) in einem Ausschnitt des Quintenzirkels (am Beispiel ausgehend von der Tonart „C“) dar, so ergibt sich der Zusammenhang zwischen den Dur- und Moll-Akkorden sowie die praktische Menge spielbarer Akkorde.
| Dur-I | Stimmungs- verhältnis | Quintenzirkel | |||
| F | C | G | D | ||
| I | 8 | F | C | G | D |
| iii | 10 | A | E | B | F#/Gb |
| V | 12 | C | G | D | A |
| viio | 15 | E | B | F#/Gb | C#/Db |
| Dur-I | Stimmungs- verhältnis | Quintenzirkel | |||
| F | C | G | D | ||
| I | 8 | 1/3 | 1 | 3 | 3*3 |
| iii | 10 | 5/3 | 5 | 3*5 | 3*3*5 |
| V | 12 | 1 | 3 | 3*3 | 3*3*3 |
| viio | 15 | 5 | 3*5 | 3*3*5 | 3*3*3*5 |
| Dur-I | Stimmungs- verhältnis | Quintenzirkel x5 | |||
| A | E | B | F#/Gb | ||
| I | 8 | A | E | B | F#/Gb |
| iii | 10 | C#/Db | G#/Ab | D#/Eb | A#/Bb |
| V | 12 | E | B | F#/Gb | C#/Db |
| viio | 15 | G#/Ab | D#/Eb | A#/Bb | F |
| Dur-I | Stimmungs- verhältnis | Quintenzirkel x5 | |||
| A | E | B | F#/Gb | ||
| I | 8 | 5/3 | 5 | 3*5 | 3*3*5 |
| iii | 10 | 5*5/3 | 5*5 | 3*5*5 | 3*3*5*5 |
| V | 12 | 5 | 3*5 | 3*3*5 | 3*3*3*5 |
| viio | 15 | 5*5 | 3*5*5 | 3*3*5*5 | 3*3*3*5*5 |
| Dur-I | Stimmungs- verhältnis | Quintenzirkel ÷5 | |||
| C#/Db | G#/Ab | D#/Eb | A#/Bb | ||
| I | 8 | C#/Db | G#/Ab | D#/Eb | A#/Bb |
| iii | 10 | F | C | G | D |
| V | 12 | G#/Ab | D#/Eb | A#/Bb | F |
| viio | 15 | C | G | D | A |
| Dur-I | Stimmungs- verhältnis | Quintenzirkel ÷5 | |||
| C#/Db | G#/Ab | D#/Eb | A#/Bb | ||
| I | 8 | 1/(3*5) | 1/5 | 3/5 | 3*3/5 |
| iii | 10 | 1/3 | 1 | 3 | 3*3 |
| V | 12 | 1/5 | 3/5 | 3*3/5 | 3*3*3/5 |
| viio | 15 | 1 | 3 | 3*3 | 3*3*3 |
| Dur-I | Quintenzirkel | ||||
| F | C | G | D | ||
| I | 8 | F | C | G | D |
| iii | 10 | A | E | B | F#/Gb |
| V | 12 | C | G | D | A |
| viio | 15 | E | B | F#/Gb | C#/Db |
| Dur-I | Quintenzirkel | ||||
| F | C | G | D | ||
| I | 8 | 1/3 | 1 | 3 | 32 |
| iii | 10 | 5/3 | 5 | 3*5 | 32*5 |
| V | 12 | 1 | 3 | 32 | 33 |
| viio | 15 | 5 | 3*5 | 32*5 | 33*5 |
| Dur-I | Quintenzirkel x5 | ||||
| A | E | B | F#/Gb | ||
| I | 8 | A | E | B | F#/Gb |
| iii | 10 | C#/Db | G#/Ab | D#/Eb | A#/Bb |
| V | 12 | E | B | F#/Gb | C#/Db |
| viio | 15 | G#/Ab | D#/Eb | A#/Bb | F |
| Dur-I | Quintenzirkel x5 | ||||
| A | E | B | F#/Gb | ||
| I | 8 | 5/3 | 5 | 3*5 | 32*5 |
| iii | 10 | 52/3 | 52 | 3*52 | 32*52 |
| V | 12 | 5 | 3*5 | 32*5 | 33*5 |
| viio | 15 | 52 | 3*52 | 32*52 | 33*52 |
| Dur-I | Quintenzirkel ÷5 | ||||
| C#/Db | G#/Ab | D#/Eb | A#/Bb | ||
| I | 8 | C#/Db | G#/Ab | D#/Eb | A#/Bb |
| iii | 10 | F | C | G | D |
| V | 12 | G#/Ab | D#/Eb | A#/Bb | F |
| viio | 15 | C | G | D | A |
| Dur-I | Quintenzirkel ÷5 | ||||
| C#/Db | G#/Ab | D#/Eb | A#/Bb | ||
| I | 8 | 1/(3*5) | 1/5 | 3/5 | 32/5 |
| iii | 10 | 1/3 | 1 | 3 | 32 |
| V | 12 | 1/5 | 3/5 | 32/5 | 33/5 |
| viio | 15 | 1 | 3 | 32 | 33 |
| Dur-II | Stimmungs- verhältnis | Quintenzirkel | |||
| F | C | G | D | ||
| I | 20 | F | C | G | D |
| iii | 25 | A | E | B | F#/Gb |
| V | 30 | C | G | D | A |
| VII | 36 | D#/Eb | A#/Bb | F | C |
| Dur-II | Stimmungs- verhältnis | Quintenzirkel | |||
| F | C | G | D | ||
| I | 20 | 1/3 | 1 | 3 | 3*3 |
| iii | 25 | 5/3 | 5 | 3*5 | 3*3*5 |
| v | 30 | 1 | 3 | 3*3 | 3*3*3 |
| VII | 36 | 3/5 | 3*3/5 | 3*3*3/5 | 3*3*3*3/5 |
| Dur-II | Stimmungs- verhältnis | Quintenzirkel x5 | |||
| A | E | B | F#/Gb | ||
| I | 20 | A | E | B | F#/Gb |
| iii | 25 | C#/Db | G#/Ab | D#/Eb | A#/Bb |
| v | 30 | E | B | F#/Gb | C#/Db |
| VII | 36 | G | D | A | E |
| Dur-II | Stimmungs- verhältnis | Quintenzirkel x5 | |||
| A | E | B | F#/Gb | ||
| I | 20 | 5/3 | 5 | 3*5 | 3*3*5 |
| iii | 25 | 5*5/3 | 5*5 | 3*5*5 | 3*3*5*5 |
| v | 30 | 5 | 3*5 | 3*3*5 | 3*3*3*5 |
| VII | 36 | 3 | 3*3 | 3*3*3 | 3*3*3*3 |
| Dur-II | Stimmungs- verhältnis | Quintenzirkel ÷5 | |||
| C#/Db | G#/Ab | D#/Eb | A#/Bb | ||
| I | 20 | C#/Db | G#/Ab | D#/Eb | A#/Bb |
| iii | 25 | F | C | G | D |
| V | 30 | G#/Ab | D#/Eb | A#/Bb | F |
| VII | 36 | B | F#/Gb | C#/Db | G#/Ab |
| Dur-II | Stimmungs- verhältnis | Quintenzirkel ÷5 | |||
| C#/Db | G#/Ab | D#/Eb | A#/Bb | ||
| I | 20 | 1/(3*5) | 1/5 | 3/5 | 3*3/5 |
| iii | 25 | 1/3 | 1 | 3 | 3*3 |
| v | 30 | 1/5 | 3/5 | 3*3/5 | 3*3*3/5 |
| VII | 36 | 3/(5*5) | 3*3/(5*5) | 3*3*3/(5*5) | 3*3*3*3/(5*5) |
| Dur-II | Quintenzirkel | ||||
| F | C | G | D | ||
| I | 20 | F | C | G | D |
| iii | 25 | A | E | B | F#/Gb |
| V | 30 | C | G | D | A |
| VII | 36 | D#/Eb | A#/Bb | F | C |
| Dur-II | Quintenzirkel | ||||
| F | C | G | D | ||
| I | 20 | 1/3 | 1 | 3 | 32 |
| iii | 25 | 5/3 | 5 | 3*5 | 32*5 |
| v | 30 | 1 | 3 | 32 | 33 |
| VII | 36 | 3/5 | 32/5 | 33/5 | 34/5 |
| Dur-II | Quintenzirkel x5 | ||||
| A | E | B | F#/Gb | ||
| I | 20 | A | E | B | F#/Gb |
| iii | 25 | C#/Db | G#/Ab | D#/Eb | A#/Bb |
| v | 30 | E | B | F#/Gb | C#/Db |
| VII | 36 | G | D | A | E |
| Dur-II | Quintenzirkel x5 | ||||
| A | E | B | F#/Gb | ||
| I | 20 | 5/3 | 5 | 3*5 | 32*5 |
| iii | 25 | 52/3 | 52 | 3*52 | 32*52 |
| v | 30 | 5 | 3*5 | 32*5 | 33*5 |
| VII | 36 | 3 | 32 | 33 | 34 |
| Dur-II | Quintenzirkel ÷5 | ||||
| C#/Db | G#/Ab | D#/Eb | A#/Bb | ||
| I | 20 | C#/Db | G#/Ab | D#/Eb | A#/Bb |
| iii | 25 | F | C | G | D |
| V | 30 | G#/Ab | D#/Eb | A#/Bb | F |
| VII | 36 | B | F#/Gb | C#/Db | G#/Ab |
| Dur-II | Quintenzirkel ÷5 | ||||
| C#/Db | G#/Ab | D#/Eb | A#/Bb | ||
| I | 20 | 1/(3*5) | 1/5 | 3/5 | 32/5 |
| iii | 25 | 1/3 | 1 | 3 | 32 |
| v | 30 | 1/5 | 3/5 | 32/5 | 33/5 |
| VII | 36 | 3/52 | 32/52 | 33/52 | 34/52 |
| Moll-I | Stimmungs- verhältnis | Quintenzirkel | |||
| f | c | g | d | ||
| i | 10 | F | C | G | D |
| III | 12 | G#/Ab | D#/Eb | A#/Bb | F |
| v | 15 | C | G | D | A |
| VII | 18 | D#/Eb | A#/Bb | F | C |
| Moll-I | Stimmungs- verhältnis | Quintenzirkel | |||
| f | c | g | d | ||
| i | 10 | 1/3 | 1 | 3 | 3*3 |
| III | 12 | 1/5 | 3/5 | 3*3/5 | 3*3*3/5 |
| v | 15 | 1 | 3 | 3*3 | 3*3*3 |
| VII | 18 | 3/5 | 3*3/5 | 3*3*3/5 | 3*3*3*3/5 |
| Moll-I | Stimmungs- verhältnis | Quintenzirkel x5 | |||
| a | e | b | f#/gb | ||
| i | 10 | A | E | B | F#/Gb |
| III | 12 | C | G | D | A |
| v | 15 | E | B | F#/Gb | C#/Db |
| VII | 18 | G | D | A | E |
| Moll-I | Stimmungs- verhältnis | Quintenzirkel x5 | |||
| a | e | b | f#/gb | ||
| i | 10 | 5/3 | 5 | 3*5 | 3*3*5 |
| III | 12 | 1 | 3 | 3*3 | 3*3*3 |
| v | 15 | 5 | 3*5 | 3*3*5 | 3*3*3*5 |
| VII | 18 | 3 | 3*3 | 3*3*3 | 3*3*3*3 |
| Moll-I | Stimmungs- verhältnis | Quintenzirkel ÷5 | |||
| c#/db | g#/ab | d#/eb | a#/bb | ||
| i | 10 | C#/Db | G#/Ab | D#/Eb | A#/Bb |
| III | 12 | E | B | F#/Gb | C#/Db |
| v | 15 | G#/Ab | D#/Eb | A#/Bb | F |
| VII | 18 | B | F#/Gb | C#/Db | G#/Ab |
| Moll-I | Stimmungs- verhältnis | Quintenzirkel ÷5 | |||
| c#/db | g#/ab | d#/eb | a#/bb | ||
| i | 10 | 1/(3*5) | 1/5 | 3/5 | 3*3/5 |
| III | 12 | 1/(5*5) | 3/(5*5) | 3*3/(5*5) | 3*3*3/(5*5) |
| v | 15 | 1/5 | 3/5 | 3*3/5 | 3*3*3/5 |
| VII | 18 | 3/(5*5) | 3*3/(5*5) | 3*3*3/(5*5) | 3*3*3*3/(5*5) |
| Moll-I | Quintenzirkel | ||||
| f | c | g | d | ||
| i | 10 | F | C | G | D |
| III | 12 | G#/Ab | D#/Eb | A#/Bb | F |
| v | 15 | C | G | D | A |
| VII | 18 | D#/Eb | A#/Bb | F | C |
| Moll-I | Quintenzirkel | ||||
| f | c | g | d | ||
| i | 10 | 1/3 | 1 | 3 | 32 |
| III | 12 | 1/5 | 3/5 | 32/5 | 33/5 |
| v | 15 | 1 | 3 | 32 | 33 |
| VII | 18 | 3/5 | 32/5 | 33/5 | 34/5 |
| Moll-I | Quintenzirkel x5 | ||||
| a | e | b | f#/gb | ||
| i | 10 | A | E | B | F#/Gb |
| III | 12 | C | G | D | A |
| v | 15 | E | B | F#/Gb | C#/Db |
| VII | 18 | G | D | A | E |
| Moll-I | Quintenzirkel x5 | ||||
| a | e | b | f#/gb | ||
| i | 10 | 5/3 | 5 | 3*5 | 32*5 |
| III | 12 | 1 | 3 | 32 | 33 |
| v | 15 | 5 | 3*5 | 32*5 | 33*5 |
| VII | 18 | 3 | 32 | 33 | 34 |
| Moll-I | Quintenzirkel ÷5 | ||||
| c#/db | g#/ab | d#/eb | a#/bb | ||
| i | 10 | C#/Db | G#/Ab | D#/Eb | A#/Bb |
| III | 12 | E | B | F#/Gb | C#/Db |
| v | 15 | G#/Ab | D#/Eb | A#/Bb | F |
| VII | 18 | B | F#/Gb | C#/Db | G#/Ab |
| Moll-I | Quintenzirkel ÷5 | ||||
| c#/db | g#/ab | d#/eb | a#/bb | ||
| i | 10 | 1/(3*5) | 1/5 | 3/5 | 32/5 |
| III | 12 | 1/52 | 3/52 | 32/52 | 33/52 |
| v | 15 | 1/5 | 3/5 | 32/5 | 33/5 |
| VII | 18 | 3/52 | 32/52 | 33/52 | 34/52 |
| Moll-II | Stimmungs- verhältnis | Quintenzirkel | |||
| f | c | g | d | ||
| i | 40 | F | C | G | D |
| III | 48 | G#/Ab | D#/Eb | A#/Bb | F |
| v | 60 | C | G | D | A |
| viio | 75 | E | B | F#/Gb | C#/Db |
| Moll-II | Stimmungs- verhältnis | Quintenzirkel | |||
| f | c | g | d | ||
| i | 40 | 1/3 | 1 | 3 | 3*3 |
| III | 48 | 1/5 | 3/5 | 3*3/5 | 3*3*3/5 |
| v | 60 | 1 | 3 | 3*3 | 3*3*3 |
| viio | 75 | 5 | 3*5 | 3*3*5 | 3*3*3*5 |
| Moll-II | Stimmungs- verhältnis | Quintenzirkel x5 | |||
| a | e | b | f#/gb | ||
| i | 40 | A | E | B | F#/Gb |
| III | 48 | C | G | D | A |
| v | 60 | E | B | F#/Gb | C#/Db |
| viio | 75 | G#/Ab | D#/Eb | A#/Bb | F |
| Moll-II | Stimmungs- verhältnis | Quintenzirkel x5 | |||
| a | e | b | f#/gb | ||
| i | 40 | 5/3 | 5 | 3*5 | 3*3*5 |
| III | 48 | 1 | 3 | 3*3 | 3*3*3 |
| v | 60 | 5 | 3*5 | 3*3*5 | 3*3*3*5 |
| viio | 75 | 5*5 | 3*5*5 | 3*3*5*5 | 3*3*3*5*5 |
| Moll-II | Stimmungs- verhältnis | Quintenzirkel ÷5 | |||
| c#/db | g#/ab | d#/eb | a#/bb | ||
| i | 40 | C#/Db | G#/Ab | D#/Eb | A#/Bb |
| III | 48 | E | B | F#/Gb | C#/Db |
| v | 60 | G#/Ab | D#/Eb | A#/Bb | F |
| viio | 75 | C | G | D | A |
| Moll-II | Stimmungs- verhältnis | Quintenzirkel ÷5 | |||
| c#/db | g#/ab | d#/eb | a#/bb | ||
| i | 40 | 1/(3*5) | 1/5 | 3/5 | 3*3/5 |
| III | 48 | 1/(5*5) | 3/(5*5) | 3*3/(5*5) | 3*3*3/(5*5) |
| v | 60 | 1/5 | 3/5 | 3*3/5 | 3*3*3/5 |
| viio | 75 | 1 | 3 | 3*3 | 3*3*3 |
| Moll-II | Quintenzirkel | ||||
| f | c | g | d | ||
| i | 40 | F | C | G | D |
| III | 48 | G#/Ab | D#/Eb | A#/Bb | F |
| v | 60 | C | G | D | A |
| viio | 75 | E | B | F#/Gb | C#/Db |
| Moll-II | Quintenzirkel | ||||
| f | c | g | d | ||
| i | 40 | 1/3 | 1 | 3 | 32 |
| III | 48 | 1/5 | 3/5 | 32/5 | 33/5 |
| v | 60 | 1 | 3 | 32 | 33 |
| viio | 75 | 5 | 3*5 | 32*5 | 33*5 |
| Moll-II | Quintenzirkel x5 | ||||
| a | e | b | f#/gb | ||
| i | 40 | A | E | B | F#/Gb |
| III | 48 | C | G | D | A |
| v | 60 | E | B | F#/Gb | C#/Db |
| viio | 75 | G#/Ab | D#/Eb | A#/Bb | F |
| Moll-II | Quintenzirkel x5 | ||||
| a | e | b | f#/gb | ||
| i | 40 | 5/3 | 5 | 3*5 | 32*5 |
| III | 48 | 1 | 3 | 32 | 33 |
| v | 60 | 5 | 3*5 | 32*5 | 33*5 |
| viio | 75 | 52 | 3*52 | 32*52 | 33*52 |
| Moll-II | Quintenzirkel ÷5 | ||||
| c#/db | g#/ab | d#/eb | a#/bb | ||
| i | 40 | C#/Db | G#/Ab | D#/Eb | A#/Bb |
| III | 48 | E | B | F#/Gb | C#/Db |
| v | 60 | G#/Ab | D#/Eb | A#/Bb | F |
| viio | 75 | C | G | D | A |
| Moll-II | Quintenzirkel ÷5 | ||||
| c#/db | g#/ab | d#/eb | a#/bb | ||
| i | 40 | 1/(3*5) | 1/5 | 3/5 | 32/5 |
| III | 48 | 1/52 | 3/52 | 32/52 | 33/52 |
| v | 60 | 1/5 | 3/5 | 32/5 | 33/5 |
| viio | 75 | 1 | 3 | 32 | 33 |
Die in den Tabellen weiß hinterlegten Stimmungsverhältnisse sind in der Reinen Stimmung nicht verfügbar.
Obwohl einige Akkorde in der Reinen Stimmung theoretisch nicht präzise abgebildet werden können, werden bestimmte Akkorde wie beispielsweise der auf der Terz des Grundtons (in diesem Beispiel „C“) aufbauende Dominantseptakkord (entsprechend „E Dur-II“) in der Praxis gerne verwendet.
Dies wird durch die effektive Annäherung an die exakten Saitenverhältnisse und die grundsätzliche Approximation der Notenwerte durch die Gleichstufige Stimmung ermöglicht.
Umgekehrt gibt es Akkorde, die zwar in der Reinen Stimmung gebildet werden können, aber sich durch die Gleichstufige Stimmung im Zusammenhang mit der verwendeten Tonart weniger gut spielen lassen.
Weitere (Reine) Akkorde
In der klassischen Musiktheorie gibt es noch eine große Menge weiterer festgelegter Akkord-Bezeichnungen, die auf unterschiedlichsten Kombinationen von Saitenverhältnissen sowie der Logik der Reinen Stimmung mit ihrer Anordnung im Quintenzirkel basieren.
Beispielsweise findet sich die Grundlage für die sogenannte Dur-Moll-Austauschbarkeit (engl. „Modal Interchange“ oder „Borrowed Chords“) in der Reinen Stimmung wieder – ebenso wie die Bildung von Sus-Akkorden (engl. „Suspended Chords“).
| Bezeichnung | Abkürzung | Akkord | Stimmungsverhältnis |
| Sus-2-Akkord | Sus-2 | I – ii – V | 9:8:12 |
| Sus-4-Akkord | Sus-4 | I – IV – V | 6:8:9 |
| Bez. | Akkord | Stimm.- verhältnis |
| Sus-2 | I – ii – V | 9:8:12 |
| Sus-4 | I – IV – V | 6:8:9 |
Die Sus-Akkorde für das Beispiel „C Dur“ sind „C – F – G“ (Sus-4) und „C – D – G“ (Sus-2). Man sieht, dass diese Noten sowohl nebeneinander als auch im selben Abschnitt des Quintenzirkels liegen und somit im Innenverhältnis nur aus reinen Quinten bestehen.
Digitales Tuning
Leider lässt sich ein Klavier nicht so stimmen, dass die Reinen Stimmungen für alle Tonarten (im Quintenzirkel bzw. auf der Tastatur) gleichzeitig gelten – was wohl auch der Grund dafür ist, dass sich historisch verschiedenste Stimmungssysteme gebildet haben, bis sich die Gleichstufige Stimmung als Kompromiss etabliert hat.
Im heutigen digitalen Zeitalter ist man jedoch nichtmehr zwangsweise darauf angewiesen ist, ein Klavier mit viel manuellem Aufwand so zu stimmen, damit es an einem Konzertabend verschiedene Lieder in unterschiedlichen Tonarten spielen kann – denn mit Hilfe von Plugins lassen sich in „Digital Audio Workstations“ („DAWs“) längst allerlei Instrumente virtuell simulieren und häufig auch das Stimmsystem modifizieren.
Häufig findet man die Reine Stimmung (engl. „Just Intonation“) bereits unter den voreingestellten Auswahlmöglichkeiten.
Alternativ gibt es in einigen Programmen auch die Möglichkeit eigene Stimmsysteme mit Hilfe von Scala .scl oder AnaMark Tuning Files .tun zu implementieren.
| Reine Stimmung (Prime = C4 = 261,63 Hz) | |
| Scala .scl | AnaMark .tun |
| ! Just Intonation 12 ! 16/15 9/8 6/5 5/4 4/3 45/32 3/2 8/5 5/3 9/5 15/8 2/1 | ; Just Intonation (note 60: C=261.63 Hz; 1:1) ; AnaMark section [Exact Tuning] note 0=0.0000 note 1=111.7313 note 2=203.9100 note 3=315.6413 note 4=386.3137 note 5=498.0450 note 6=590.2237 note 7=701.9550 note 8=813.6863 note 9=884.3587 note 10=1017.5963 ... note 127=12701.9550 |
| Gleichstufige Stimmung (A4 = 440 Hz) | |
| Scala .scl | AnaMark .tun |
| ! Equal Temperament (A=440 Hz) 12 ! 100.000 cents 200.000 cents 300.000 cents 400.000 cents 500.000 cents 600.000 cents 700.000 cents 800.000 cents 900.000 cents 1000.000 cents 1100.000 cents 1200.000 cents | ; Equal Temperament (note 69: A=440 Hz) ; AnaMark section [Exact Tuning] note 0=0.0000 note 1=100.0000 note 2=200.0000 note 3=300.0000 note 4=400.0000 note 5=500.0000 note 6=600.0000 note 7=700.0000 note 8=800.0000 note 9=900.0000 note 10=1000.0000 ... note 127=12700.0000 |
| Gleichstufige Stimmung (A4 = 432 Hz) | |
| Scala .scl | AnaMark .tun |
| ! Equal Temperament (A=432 Hz) 12 ! 68.233 cents 168.233 cents 268.233 cents 368.233 cents 468.233 cents 568.233 cents 668.233 cents 768.233 cents 868.233 cents 968.233 cents 1068.233 cents 1168.233 cents | ; Equal Temperament (note 69: A=432 Hz) ; AnaMark section [Exact Tuning] note 0=-31.7667 note 1=68.2333 note 2=168.2333 note 3=268.2333 note 4=368.2333 note 5=468.2333 note 6=568.2333 note 7=668.2333 note 8=768.2333 note 9=868.2333 note 10=968.2333 ... note 127=12668.2333 |
Besonderer Tipp für Logic Pro X User
Mit einer Scala .scl Datei lässt sich Logic Pro in den Projekt-Einstellungen für alle Standard-Plugins einstellen. Es gibt allerdings ein paar Einschränkungen zu berücksichtigen.
Beispielsweise dürfen die einzelnen den Tasten zugewiesenen Verhältnisse zu keiner Abweichung größer +/- 100 Cents von der Gleichstufigen Stimmung (ausgehend vom Kammerton A4 = 440 Hz) führen. Zusätzlich muss in Logic Pro eine beliebige Note aus der Gleichstufigen Stimmung ausgewählt werden, von welcher ausgehend die Stimmungsverhältnisse berechnet werden. Entspricht C4 = 261,53 Hz (in AnaMark: note 69 = 6000.0000 bzw. note 0 = 0.0000) etwa dem Verhältnis 1:1, so folgt z.B. A4 = 436,04 Hz als Große Sexte mit dem Verhältnis 3:5 (in Scala: 5/3).
Zusätzlich kann man die Stimmung (unter „Software Instrument Pitch“) noch um +/- 100 Cents verschieben und somit jede beliebige Grundfrequenz einstellen.
In der Regel übernehmen Plugins von Drittanbietern nicht die „Tuning“-Einstellungen von Logic Pro und müssen individuell eingestellt werden. Beispielsweise lässt sich die Tonleiter in Omnisphere von Spectrasonics mit einer AnaMark .tun Datei in den Systemeinstellungen individuell anpassen.
Vergleich
Zum Vergleich zwischen der Gleichstufigen Stimmung und der Reinen Stimmung finden sich im Folgenden verschiedene Akkord-Beispiele:
Mit einem normalen Ohr lässt sich kaum ein Unterschied zwischen der Gleichstufigen und der Reinen Stimmung erkennen. Erst wenn man die jeweiligen korrespondierenden Töne parallel abspielt, lässt sich der feine Unterschied zwischen den Frequenzwerten deutlich erkennen.